查询时，先将所有恒定贡献求或
从高位开始查询所有位置，判断是否有 (2) 类贡献
若没有 (2) 类贡献，跳过
若有 2 个 (2) 类贡献，或这这一位已经为 1，则从这一位往后都直接给 1 (对应 (ii))
若只有一个，设为 $y$，则依次考虑当前答案中为 $0$ 的位，能给 1 就给 1 (对应 (i))。

#include <cstdio>
 
const int N = 2e5 + 10;
 
int T, n, m;
int c[N][30], z[N][30], lst[N][30];
int s[N];
 
int all(int n) { return (1 << n) - 1; }
int lg(int x) { return 31 - __builtin_clz(x); }
 
int main() {
	for(scanf("%d", &T); T--; ) {
		scanf("%d", &n);
		for(int i = 1, x, y; i <= n; ++i) {
			scanf("%d%d", &x, &y);
			int l = x & ~all(lg(x ^ y) + 1);
			for(int j = 0; j < 30; ++j) 
				c[i][j] = c[i - 1][j] + ((l >> j) & 1),
				z[i][j] = z[i - 1][j],
				lst[i][j] = lst[i - 1][j];
			y ^= l;
			if(y) {
				int t = 31 - __builtin_clz(y);
				lst[i][t] = y, z[i][t]++;
			}
		}
		scanf("%d", &m);
		for(int i = 1, l, r; i <= m; ++i) {
			scanf("%d%d", &l, &r), l--;
			int ans = 0;
			for(int j = 0; j < 30; ++j) ans |= (c[r][j] > c[l][j]) << j;
			for(int j = 29; ~j; --j) if(z[r][j] > z[l][j]) {
				int t = lst[r][j];
				if(z[r][j] > z[l][j] + 1) {
					ans |= all(j + 1);
					break;
				}
				/*for(int k = j; ~k; --k) if(t & (1 << k)) {
					if(ans & (1 << k)) {
						ans |= all(k + 1);
						break;
					}
					ans |= 1 << k;
				}*/
				int w = t & ~ans;
				ans |= w, t -= w;
				if(t) ans |= all(lg(t));
			}
			printf("%d ", ans);
		}
		puts("");
	}
}

Solution2

设两部分分别为 $f,g=y$，考虑如何合并 (1) $f$ 直接或合并 (2) $g$ 在合并时，可以先做或，如果有重叠的位，将其中一个的这一位舍掉可以把下面的所有位都赋 1。

#include <cstdio>

const int N = 2e5 + 10;

char buf[200000], *p1, *p2;
#define getchar() (((p1==p2)&&(p2=(p1=buf)+fread(buf,1,200000,stdin))),*p1++)
int rd() {
	int x = 0; char c;
	while(c = getchar(), c < 48);
	do x = x * 10 + (c - 48);
	while(c = getchar(), c > 47);
	return x;
}

int n, k;
int all(int n) { return (1 << n) - 1; }
int lg(int x) { return 31 - __builtin_clz(x); }
int uor(int x, int y) {
	int z = x | y;
	if(x & y) z |= all(lg(x & y));
	return z;
}
int f[N << 2], g[N << 2];
int sf, sg;

int main() {
	for(int T = rd(); T--; ){
		for(n = rd(), k = 1; k <= n + 1; k <<= 1);
		for(int i = 0; i < k; ++i) f[k + i] = g[k + i] = 0;
		for(int i = 1; i <= n; ++i) {
			int x = rd(), y = rd();
			int t = x & ~all(lg(x ^ y) + 1);
			f[k + i] = t, g[k + i] = y ^ t;
		}
		for(int i = k - 1; i; --i) {
			f[i] = f[i << 1] | f[i << 1 | 1];
			g[i] = uor(g[i << 1], g[i << 1 | 1]);
		}
		for(int m = rd(); m--; ) {
			sf = sg = 0;
			for(int l = rd() + k - 1, r = rd() + k + 1; l ^ r ^ 1; l >>= 1, r >>= 1) {
				if(~l & 1) {
					sf |= f[l ^ 1];
					sg |= uor(sg, g[l ^ 1]);
				}
				if(r & 1) {
					sf |= f[r ^ 1];
					sg |= uor(sg, g[r ^ 1]);
				}
			}
			printf("%d ", uor(sf, sg));
		}
		puts("");
	}
}

Probabilistic Method

Posted on 2024-01-10 Edited on 2024-04-19 In 课程笔记

Probabilistic Method

符号约定

均值：$\mu=\mathbb{E}[X]$

方差：$\sigma=\text{Var}[X]$.

斜方差：$\text{Cov}(X,Y)$.

引入

对于 0/1 随机变量 $X_i$（也对应着一个事件是否发生），令 $X=\sum X_i$，考虑如下显然的性质：

\[ \Pr[\bigvee X_i]=\Pr[X\ge 1]\leq \mathbb{E}[X] \] (Markov Inequality)

由此，当 $\mathbb{E}[X]\to 0$ 时，我们可以说几乎所有事件 $X_i$ 都不发生。

这个 bound 非常松，但是由于计算期望比计算所有事件发生的概率容易的多，在很多场景下用于简单估计。

一类问题的刻画

本文中用如下的问题来讲解 Probabilistic Method。

假设有随机图： $G(n,p)$：$|V|=n$，所有 $\binom{n}{2}$ 条边独立，以 $p$ 的概率出现。

有性质：$A: \mathbb{G} \to \{0,1\}$，例如 $A:$ $G$ 含有一个三元环。

很显然，当 $p$ 越大，$A(G)$ 成立的概率也越高，我们希望找到一个 $p_n$，使得：

当 $p\gg p_n$ 时，$\Pr[A(G)] \to 1$。
当 $p\ll p_n$ 时，$\Pr[A(G)]\to 0$。

这样的一个 threshold 在估计特定问题时效果非常好，比如：在特定温度考虑一个物质的结构，可以认为其中的每一个分子团之间有 $p$ 的概率有边，当 $n\to +\infty$ 时，通过描述图的大致形态来分析相态变化。

这里对于 $p_n$ 存在性给出定理：

Theorem(Bollobas, Thomason, 1987): 对于所有单调增的性质 $A$，$p_n$ 总存在。单调增的定义：在满足性质的图上加入一条边依然满足性质，即 $A(G)\implies A(G\cup \{e\})$

Theorem (Glebskii et al 1969, Fagin 1976) 对于任何固定的 $p\in (0,1)$，若 $A$ 可以用一阶逻辑表示，则 $\lim_{n\to+\infty} \Pr[G(n,p)\vDash A]=0 / 1$ (定理说明常数无法作为 threshold)

Theorem (Shelah and Spencer, 1988) 对于任何非有理数 $\alpha\in (0,1)$, $p_n=\frac{1}{n^{\alpha}}$, 若 $A$ 可以用一阶逻辑表示, $\lim_{n\to+\infty} P(G(n,p)\vDash A)=0 / 1$ (定理说明 $\frac{1}{n^{\alpha}}$ 无法作为 threshold)

First Moment Method

第一类概率方法的核心即引子里提到的 $\Pr[\bigvee X]\leq \mu$。

考虑用这个方法来估计三元环出现的概率，令 $X_i$ 表示图中任意三个点之间成环。

则 $\mu=\binom{n}{3} p^3\sim (np)^3$，故当 $p=o(n^{-1})$ 时，$\mu \to 0$，即图中几乎不可能出现三元环。

期望的估计固然简单，但是也存在显然的缺陷，比如：

若 $\Pr[X=0]=1-\frac{1}{n},\Pr[X=n^2]=\frac{1}{n}$,
则： $\mathbb{E}>1,\Pr[X\ge 1]\to 0$. (期望容易受到一个特殊单点的影响)。

Second Moment Method

第二类概率方法用于估计 $\Pr[X= 0]\to 0$，即证明 threshold 的另一边。

由 Chebyshev Inequality: $\Pr[|X-\mu|\ge \lambda \sigma]\leq\frac{1}{\lambda^2}$
则 $\Pr[X=0]\leq P(|X-\mu|\ge \mu)\leq \frac{\sigma^2}{\mu^2}=\frac{\mathbb{E}(X^2)}{\mathbb{E}(X)^2}-1$

由 Cauthy inequality: $(\mathbb{E}(X))^2\leq \Pr[X\ge 1]\cdot \mathbb{E}(X^2)$
则 $\Pr[X=0]\leq \frac{\sigma^2}{\mathbb{E}(X^2)}=1-\frac{\mathbb{E}(X)^2}{\mathbb{E}(X^2)}$

这样我们就可以通过计算 $\mathbb{E}[X]$ 和 $\mathbb{E}[X^2]$ 来估计 $\Pr[X=0]$ 的上界。

不过有时候计算 $\mathbb{E}[X^2]$ 并不是容易事，这里我们也可以总结出一些条件。

$\sigma^2=\sum \text{Var}(X_i)^2 +\sum_{i\ne j} \text{Cov}(X_i,X_j)\xlongequal{\Delta}I_1+I_2$，我们想要 $\sigma^2=o(\mu^2)$.

$I_1=\sum\mathbb{E}(X_i^2)-\mathbb{E}(X_i)^2\leq \sum\mathbb{E}(X_i^2)$，在我们的问题中基本可以认为 $\sum \mathbb{E}(X_i^2)= o(\mu^2)$

$\begin{aligned}I_2&=\sum_{i\ne j} \text{Cov}(X_i,X_j)\\&=\sum_{i\ne j}\mathbb{E}(X_iX_j)-\mathbb{E}(X_i)\mathbb{E}(X_j)\\&=\sum_{i}\Pr[X_i] \sum_{j\ne i}(\Pr[X_j\mid X_i]-\Pr[X_j])\\&\leq \Delta^*\sum \Pr[X_i]\\&=\Delta^*\mu\end{aligned}$
where $\displaystyle \Delta^*=\max_i\{\sum_{j\ne i}\Pr[X_j\mid X_i]-\Pr[X_j]\}$

于是我们估计得 $\sigma^2= o(\mu^2)+O(\Delta^*\mu)$

只需要 $\Delta^*=o(\mu)$ 即可说明 $\Pr[X=0]\to 0$

回到三元环问题， $\mu=n^3p^3$, 每一个 $X_i$ 与 $3(n-3)$ 个 $X_j$ 相关，所以 $\Delta^*=3(n-3)(p^2-p^3)\sim np^2$

当 $p\gg n^{-1/2}$ 时，有 $\Delta^*=o(\mu)$，此时 $\Pr[X=0]\to 0$

总结

1st: 估计期望，$\mu\to 0 \implies P(X\ge 1)\to 0$
2nd: 三种方法， $\begin{cases}\sigma^2=o(\mu^2)\\\sigma^2=o(\mathbb{E}(X^2))\\\Delta^*=o(\mu)\end{cases}\implies P(X=0)\to 0$

选择背景 | Choose Background

Posted on 2023-08-14 Edited on 2024-04-19 In 帮助

选择背景 | Choose Background

点击图片选择

猜歌名工具使用指南

Posted on 2023-08-12 Edited on 2024-04-19 In 帮助

猜歌名工具使用指南

快速导览

在最底下的框里输入形如：

1 2	1. song1 2. song2

的文本，点击 Import 按钮导入歌曲列表。

点击 Sort By Length 按钮。
点击 Copy to Clipboard 按钮，将输出复制到剪贴板。
开字符：在 guess 框里输入被开的字符，然后按回车。
猜出歌：选中歌名左边的框，表示这首歌被猜出。
点击歌名最右边的框，隐藏被猜出的歌（不一定要这么干）。

集合幂级数的 $\\ln,\\exp$

Posted on 2023-08-12 Edited on 2024-04-19 In OI 笔记

集合幂级数的 $\ln,\exp$

起始：求联通子图个数。

令 $F(x)$ 为联通的生成子图个数的形式幂级数，可以简单求出 $G(x)$ 为生成子图个数的形式幂级数。

字符串的Period(周期), Border

Posted on 2023-08-12 Edited on 2024-04-19 In OI 笔记

字符串的Period(周期), Border

前置知识：$\text{kmp}$，$\text{AC}$ 自动机

约定：字符串 $S$ 的长度为 $|S|$，原串的长度为 $n$，$[l,r]$ 的子串为 $S_{l,r}$，下标从 $1$ 开始，前缀 $S_{1,i}=pre_i$，后缀 $S_{i,n}=suf_i$，设$S$ 的 $\text{Border}$ 集合为 $B(S)$，设最长的 $\text{Border}$ 为 $\text{LBorder}$。

$\text{Border}$:

定义字符串 $S$ 的一个 $\text{Border}$ 为一个满足 $pre_i=suf_{n-i+1}$ 的前缀，$S$ 和 $\emptyset$ 也是一个 $\text{Border}$。

$\text{kmp,AC}$ 自动机的 $fail$ 指针均指向当前串的 $\text{LBorder}$。

FWT (快速沃尔什变换)详解以及 K进制FWT

Posted on 2023-08-12 Edited on 2024-04-19 In OI 笔记

FWT (快速沃尔什变换)详解以及 K进制FWT

约定：$F'=FWT(F)$

卷积的问题，事实上就是要构造$F'G'=(FG)'$

我们常见的卷积，是二进制位上的or ,and ,xor

但正式来说，是集合幂指数 上的 并，交，对称差

为了说人话，这里就不带入集合幂指数的概念了

一个常识：$\sum_{T\subseteq S}(-1)^{|T|}=[S=\emptyset]$

优雅的万能欧几里得

Posted on 2023-08-12 Edited on 2024-04-19 In OI 笔记

优雅的万能欧几里得

取自 CTT 2022 Day4 T3 （或许是2021?）

问题描述

考虑用以下方法描述一个万能欧几里得问题：

有一条端点为 $(0,0)\rightarrow (A,B)$ 的有向线段 $OP$，我们认为其两端都是空的。

其中 $A,B$ 是自然数，且 $\gcd(A,B)=1$。（当 $g=\gcd(A,B)\ne 1$ 时，可以先求 $\frac{A}{g},\frac{B}{g}$ 的结果，然后将其复制 $g$ 次）。

万能欧几里得问题要维护这样的一个过程：

一开始我们有一个空字符串 $s$。
考虑点从 $O$ 移动到 $P$ 的过程：
1. 其 $x$ 坐标每经过一个整点，就向 $s$ 中加入字符 $\text{X}$。
2. 其 $y$ 坐标每经过一个整点，就向 $s$ 中加入字符 $\text{Y}$。

注意在 $O,P$ 处不加入字符。容易发现在 $\gcd(A,B)=1$ 时，不会出现同时经过 $x,y$ 上的整点。

下图是 $P=(3,5)$ 时的例子，此时的字符串为 $\text{YXYYXY}$。

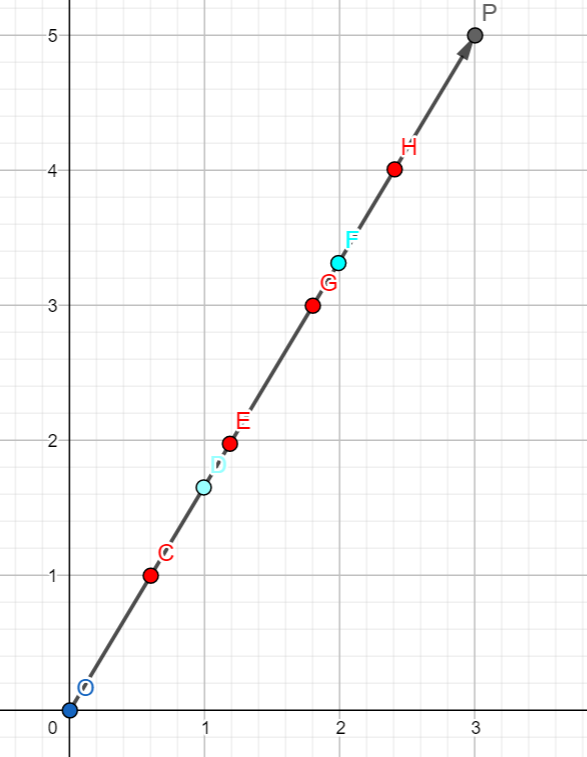
在实际的应用中，我们用 $\text{X,Y}$ 指代任何可拼接且满足结合律的操作（如矩阵）。

问题求解

用四元组 $(A,B,\text{X},\text{Y})$ 描述这样的一个万能欧几里得问题，则可以如下递归求解：

若 $B\ge A$，则每次在 $x$ 增加之前， $y$ 都会增加 $\lfloor\frac{B}{A} \rfloor$ 个，可以转化为 $(A,B\mod A,\text{Y}\cdot \lfloor\frac{B}{A} \rfloor+\text{X},\text{Y})$。
若 $B<A$，则可以直接翻转坐标系，转化为求解 $(B,A,\text{Y},\text{X})$。（而网上许多教程的翻转操作都需要处理复杂的边界条件）。

容易发现递归的问题同样是合法的万能欧几里得问题。

复杂度分析

设 $l=\lfloor\frac{B}{A} \rfloor$，递归时需要处理 $\text{Y}\cdot l$，这是一个快速幂操作，其复杂度为 $\log l$。

而 $B\mod A=B-A\cdot l\leq \frac{1}{l+1} B$，所以所有快速幂的复杂度总和为 $\log A+\log B$。

区间查询

考虑万能欧几里得的过程，容易发现其中只有两种操作：

快速幂
直接拼接

如果我们用一个节点描述一个操作，就可以用二叉树的结构维护拼接操作。

对于快速幂，只需要对于节点进行可持久化。

而万能欧几里得所产生的二叉树至多只有 $$ 层，在这样的二叉树上查询的复杂度与线段树相同。

[CF1540E - Tasty Dishes](https://codeforces.com/problemset/problem/1540/E)

Posted on 2023-08-12 Edited on 2024-04-19 In CP 题解

CF1540E - Tasty Dishes

题目大意

给定序列$a_i$，保证$|a_i|\leq i$

以及一个变换：

$\displaystyle a_i\leftarrow \sum_{j\in S_i} \max\{a_j,0\}\cdot j+\left\{\begin{aligned} a_i && a_i\leq 0 \\ i\cdot a_i && a_i>0\end{aligned}\right.$，并且保证$\forall j\in S_i,j>i$

要求维护$q$个操作：

1.查询在初始值上进行$k$轮变换后，$\sum_{i=l}^r a_i$的值

2.修改初始值，令$a_i\leftarrow a_i+x$，保证$x\ge 0$

分析

操作分析

首先观察变换的过程和修改操作，容易发现：

1.每个数$a_i$在第一个$>0$的时刻开始贡献转移，设这个时间为$d_i$

2.当一个数$a_i\leftarrow a_i+a_j\cdot j (a_j>0)$，由于$a_i\ge -i$，新的$a_i$一定$>0$

3.只有$a_i\leq 0,a_i+x>0$的情况，修改操作会对$d_i$产生影响

那么实际上我们可以在每个$a_i\leq 0,a_i+x>0$的修改时重构，由于只有$n$次重构，这一部分复杂度为$O(n^3)$

设转移矩阵$A_{i,j}=[j\in S_i\ or\ j=i] \cdot j$

设$e_i$为一个只有第$i$项为$1$的列向量

若$k\ge d_i$，则我们要求$\sum A^{k-d_i} e_i a_i$

固然不能每次都求矩阵幂，即便是预处理之后用$O(n^2\log k)$的复杂度依然不可取

加速矩阵幂

考虑到给定矩阵的特殊性，考虑用矩阵特征值来优化

由于$A$是一个上三角矩阵，那么一定满足$A_{i,i}$都是其特征值，而这题限定了$A_{i,i}=i$

故$A$有$n$个特征值，并且由于$A$是上三角矩阵，可以在$O(n^3)$时间消元得到每个$i$对应的特征向量$v_i$

模拟这个过程也容易发现，$v_i$构成的矩阵$\begin{bmatrix} \array{v_1 & v_2 &\cdots &v_n}\end{bmatrix}$是一个上三角矩阵

在所求的式子中并不存在有关$v_i$的表达式，但是有列向量$e_i$，并且$v_i$线性无关

因此我们以$n$个$v_i$作为基底替换$c$，构造矩阵$c$，满足$e_i=\sum c_{i,j} v_j$

形式化的，就是

$c \cdot \begin{bmatrix} \array{&&v_1^T &&\\ && v_2^T &&\\ &&\cdots&& \\ &&v_n^T&&}\end{bmatrix}=\begin{bmatrix} \array{&&e_1^T &&\\ && e_2^T &&\\ &&\cdots&& \\ &&e_n^T&&}\end{bmatrix}$

而右边是一个单位矩阵，故实际上这个操作就是求矩阵逆，而这个矩阵是满秩的

此时，答案式子替换为$\displaystyle \sum A^{k-d_i}\sum c_{i,j}v_ja_i$，再带入特征值的定义$Av_i=iv_i$

转化为$\displaystyle \sum a_i \sum j^{k-d_i}c_{i,j}v_j$

我们可以预处理$v_{j,k}$的前缀和，容易求得$v_{j,[l,r]}$

再将$k-d_i$参数分离，只需要维护$s_j=\sum_i a_i c_{i,j} j^{-d_i}$，所有的幂次均可以预处理得到

由于不一定满足$k\ge d_i$，因此需要用数据结构维护前缀和，复杂度为$O(qn\log n)$

如果线性预处理树状数组，则重构总复杂度为$O(n^3)$

Codeforces Submission

const int N=310,INF=1e9+10,P=1e9+7;

int n,m,q;
int a[N],A[N][N],V[N][N],SV[N][N],C[N][N];
int F[N];
ll qpow(ll x,ll k=P-2){
	ll res=1;
	for(;k;k>>=1,x=x*x%P) if(k&1) res=res*x%P;
	return res;
}
int D[N];
bitset <N> B[N],All;
struct Tree{
	int s[N],t[N];
	void clr(){ memset(t,0,(m+1)<<2); }
	void Build(){ rep(i,1,m) t[i]+=t[i-1],Mod1(t[i]),s[i]=t[i]-t[i&(i-1)],Mod2(s[i]); }
	void Add(int p,int x) {
		t[m]+=x,Mod1(t[m]);
		p++;
		while(p<=m) s[p]+=x,Mod1(s[p]),p+=p&-p;
	}
	int Que(int p) {
		int r=0;
		cmin(++p,m);
		if(p==m) return t[p];
		while(p) r+=s[p],Mod1(r),p-=p&-p;
		return r;
	}
} T[N];
int W[N][N],Inv[N][N],Pow1[N][1010],Pow2[N][1<<10];

void Make(){
	All.reset();
	rep(i,1,n) if(a[i]>0) D[i]=0,All[i]=1,All|=B[i];
	else D[i]=INF;
	m=0;
	rep(i,1,n) rep(j,1,n) if(D[j]==INF && All[j]) D[j]=i,All|=B[j];
	rep(i,1,n) if(D[i]<INF) cmax(m,D[i]);
	m++;
	rep(i,1,n) T[i].clr();
	rep(i,1,n) if(D[i]<INF) rep(j,1,n) W[i][j]=1ll*C[i][j]*Inv[j][D[i]]%P,T[j].t[D[i]+1]=(T[j].t[D[i]+1]+1ll*W[i][j]*(P+a[i]))%P;
	rep(i,1,n) T[i].Build();
}

int main() {
	n=rd();
	rep(i,1,n) {
		Inv[i][0]=1,Inv[i][1]=qpow(i);
		rep(j,2,n) Inv[i][j]=1ll*Inv[i][j-1]*Inv[i][1]%P;
	}
	rep(i,1,n) 	rep(j,*Pow1[i]=1,1000) Pow1[i][j]=1ll*Pow1[i][j-1]*i%P;
	rep(i,1,n) a[i]=rd();
	rep(i,1,n) rep(j,A[i][i]=1,rd()) A[i][rd()]=1;
	rep(i,1,n) rep(j,i+1,n) if(A[i][j]) B[j][i]=1;
	rep(i,1,n) rep(j,1,n) A[i][j]*=j;
	rep(i,1,n) drep(j,i-1,V[i][i]=1) {
		rep(k,j+1,i) V[i][j]=(V[i][j]+1ll*A[j][k]*V[i][k])%P;
		V[i][j]=V[i][j]*qpow(i-j)%P;
	}
	rep(i,1,n) rep(j,1,n) SV[i][j]=SV[i][j-1]+V[i][j],Mod1(SV[i][j]);
	rep(i,1,n) C[i][i]=1;
	rep(i,1,n) rep(j,1,i-1) rep(k,1,n) C[i][k]=(C[i][k]+1ll*(P-V[i][j])*C[j][k])%P;
	Make();
	rep(_,1,rd()) {
		int opt=rd();
		if(opt==2){
			int i=rd(),x=rd(); a[i]+=x;
			if(a[i]-x<=0 && a[i]>0) Make();
			else if(D[i]<INF && x) rep(j,1,n) T[j].Add(D[i],1ll*W[i][j]*x%P);
		} else {
			int k=rd(),l=rd(),r=rd();
			int ans=0;
			rep(j,1,n) ans=(ans+1ll*(SV[j][r]-SV[j][l-1]+P)*T[j].Que(k)%P*Pow1[j][k])%P;
			//rep(i,1,n) if(D[i]<=k) ans=(ans+1ll*w*C[i][j]%P*qpow(j,k-D[i])%P*(P+a[i]))%P;
			rep(i,l,r) if(D[i]>k) ans+=a[i],Mod2(ans);
			printf("%d\n",ans);
		}
	}
}

指路

Tools

Gallery

CF1935E Distance Learning Courses in MAC

题目大意

思路

Solution1

Solution2

Probabilistic Method

符号约定

引入

一类问题的刻画

First Moment Method

Second Moment Method

总结

选择背景 | Choose Background

猜歌名工具使用指南

快速导览

集合幂级数的 \(\ln,\exp\)

字符串的Period(周期), Border

FWT (快速沃尔什变换)详解 以及 K进制FWT

优雅的万能欧几里得

问题描述

问题求解

复杂度分析

区间查询

题目大意

分析

操作分析

加速矩阵幂

FWT (快速沃尔什变换)详解以及 K进制FWT