CF1456E - XOR-ranges

题目大意

有 \(n\) 个二进制数 \(a_i\in[L_i,R_i]\) ，给定每个二进制位的权值

序列 \(a_i\) 的权值就是 \(a_i\oplus a_{i+1}\) 二进制为权值之和

求所有满足 \(a_i\in[L_i,R_i]\) 的最小权值

分析

显然需要我们考虑对于一个数进行 数位 \(dp\) 的过程

从高位到低位，一个数要么最终都一直被限制着，要么在两个不同的位置分别解除了 \(L_i,R_i\) 的限制

容易发现， \(L_i,R_i\) 中某一个先被解除的限制一定是在第一个 \(\text{bit}(L_{i},p)\ne \text{bit}(R_i,p)\) 的位置 （实际上是小于号）

此后，选择的数一直跟着剩下的限制直到下一个位置解除

不妨考虑 \(L_i,R_i\) 中限制时间较长的一个限制，设在 \(p\) 这一位解除，那么

1. \(\exists k<p,\text{bit}(L_i,k)\ne \text{bit}(R_i,k)\)

2.如果是 \(R_i\) ，那么 \(\text{bit}(R_i,p)=1,\text{bit}(a_i,p)=0\)

如果是 \(L_i\) ，那么 \(\text{bit}(R_i,p)=0,\text{bit}(a_i,p)=1\)

如果最终每个数解除限制的位置如下

QQ截图20210519114449.png

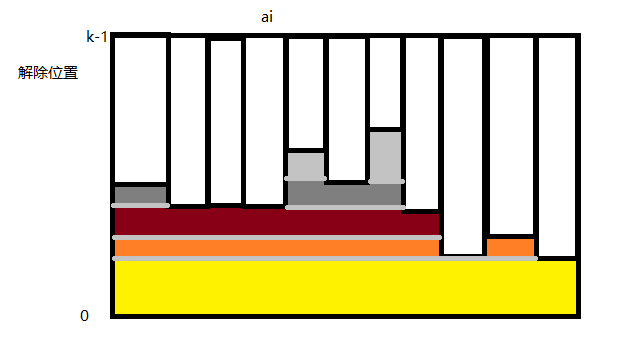
考虑他们如何对于答案贡献

对于每个二进制位，如果存在空白段，空白段的二进制可以跟随左边的段或者右边的段改变

当左边和右边最邻近的两个数这一位不同，则产生贡献

因此考虑依次扫描每一个二进制位，找到相邻可能产生贡献的 \((a_l,a_r)\)

从低位到高位，这就是一个不断将 \((a_l,a_r)\) 分裂为 \((a_l,a_k),(a_k,a_r)\) 的过程

也就是一个 笛卡尔树上的区间dp

对于当前二进制位 \(p\) 和数对 \(a_l,a_r\) ，我们需要知道的是

\(a_l\) 是受到 \(L_l\) 还是 \(R_l\) 的限制，且是否 \(p\) 这一位它解除了限制 （因为解除贡献的这一位与 \(L_l / R_l\) 相反）

\(a_r\) 是同理

转移可以直接进入下一个二进制位，计算 \(a_l,a_r\) 的贡献

或者分裂区间枚举中点 \(k\) ， \(a_k\) 恰好在这一位解除限制（或者 \(a_k\) 一直都没有解除限制，此时 \(p=0\) ）

此时 \(L_k,R_k\) 必然满足前面提到的限制，并且根据 \(\text{bit}(L_k,p)\) 和 \(\text{bit}(R_k,p)\) 枚举 \(k\) 受到 \(L_k\) 或者 \(R_k\) 的限制

const int N=55;

int n,k;
ll L[N][2],C[N];
ll dp[N][N][N][2][2][2][2];
int bit(ll x,int p){ return (x>>p)&1; }
ll dfs(int p,int l,int r,int f,int x,int g,int y){
	if(p==k) return r-l==1?0:1e18;
	ll &res=dp[p][l][r][f][x][g][y];
	if(~res) return res;
	res=dfs(p+1,l,r,f,0,g,0)+(l && r<=n && (x^y^bit(L[l][f]^L[r][g],p)))*C[p];
	rep(k,l+1,r-1) {
        // a[k] is limited all time
		if(!p) rep(j,0,1) cmin(res,dfs(p,l,k,f,x,j,0)+dfs(p,k,r,j,0,g,y));
        // a[k] frees at p
		if((L[k][0]^L[k][1])>>(p+1)) { // L,R has some different bits before p
			rep(j,0,1) if(bit(L[k][j],p)==j) 
				cmin(res,dfs(p,l,k,f,x,j,1)+dfs(p,k,r,j,1,g,y));
		}
	}
	return res;
}

int main(){
	scanf("%d%d",&n,&k);
	rep(i,1,n) rep(j,0,1) scanf("%lld",L[i]+j);
	rep(i,0,k-1) scanf("%lld",C+i);
	memset(dp,-1,sizeof dp);
	printf("%lld\n",dfs(0,0,n+1,0,0,0,0));
}