「CCO 2020」千山万壑

Posted on Edited on In

「CCO 2020」千山万壑

性质推演

推论1:不选择非树边时，答案为 \(2(n-1)-\) 直径长

比较明显就不证了

推论2:最多只会选择一条非树边

考虑如果选择两条非树边，此时必然有答案 \(\ge n-1+3\lceil\frac{n}{3}\rceil\)

因为能够选择这样的非树边，则必然存在一条长度 \(>\frac{n}{3}\) 的路径，也就是说

直径长度 \(>\frac{n}{3}\) ，故此时选择直径更优

因此不会选择两条非树边

\[ \ \]

答案计算

下称起点终点路径 \((s,t)\) ，选择的边为 \((u,v,w)\)

如果 \((s,t)\) 与 \((u,v)\) 无交，则无序额外计算贡献，此时贡献为

\(2(n-1)-dis(s,t)-(dis(u,v)-w)\)

当 \((s,t)\) 与 \((u,v)\) 有交时，设交长度为 \(len\) ，则需要额外花费 \(2(len-1)\) 的代价取遍历交部分的点

\[ \ \]

求解

显然我们需要先知道 \(dis(u,v)\) ，可以 \(O(n)\) 预处理，我们选择的非树边一定满足 \(dis(u,v)>w\)

考虑抽直径构成序列 \(L_i\) ，然后考虑每一条非树边 \((u,v,w)\) 的贡献，设 \(u,v\) 在直径上对应根的编号为 \(x,y\)

如果 \(x=y\) ，显然可以选择直径，下面讨论 \(x<y\) 的情况

  1. \((s,t)\) 与 \((u,v)\) 无交

1-1.对于 \((u,v)\) 之间的部分可以区间查询最值

1-2.两边预处理前缀/后缀最值

1-3.直径连接到 \(u\) ， \(v\) 子树的部分的答案可以换根 \(dp\) 预处理

  1. \((s,t)\) 与 \((u,v)\) 有交，设交部分在直径上的区间为 \([l,r]\)

2-1. 相交跨过直径上多个点

2-1-1.若 \(x<l<r<y\) ，此时容易用线段树维护答案

2-1-2. 若 \(x<y , \text{and } (l=x \text{ or } r=y)\) ，此时显然两边部分最优一定是选择在直径上的部分

以下情况一定不优

另一边的答案可以在线段树上查询出来，是一个区间的前缀/后缀

2-2.若 \(l=r\) ，此时 \(l=x\) 或 \(l=y\) ，且在 \([u,x],[v,y]\) 部分有交

容易发现，此时确定 \((s,t)\) 一边一定在直径的一端，另一端 \(x,y\) 对应的子树中

同样可以通过换根 \(dp\) 解决

区间查询，如果使用线段树解决，复杂度为 \(O(n+m\log n)\)

如果用奇怪数据结构（猫树），复杂度为 \(O(n\log n+m)\)

「CCO 2020」千山万壑

性质推演

推论1:不选择非树边时，答案为 \(2(n-1)-\) 直径长

比较明显就不证了

推论2:最多只会选择一条非树边

考虑如果选择两条非树边，此时必然有答案 \(\ge n-1+3\lceil\frac{n}{3}\rceil\)

因为能够选择这样的非树边，则必然存在一条长度 \(>\frac{n}{3}\) 的路径，也就是说

直径长度 \(>\frac{n}{3}\) ，故此时选择直径更优

因此不会选择两条非树边

\[ \ \]

答案计算

下称起点终点路径 \((s,t)\) ，选择的边为 \((u,v,w)\)

如果 \((s,t)\) 与 \((u,v)\) 无交，则无序额外计算贡献，此时贡献为

\(2(n-1)-dis(s,t)-(dis(u,v)-w)\)

当 \((s,t)\) 与 \((u,v)\) 有交时，设交长度为 \(len\) ，则需要额外花费 \(2(len-1)\) 的代价取遍历交部分的点

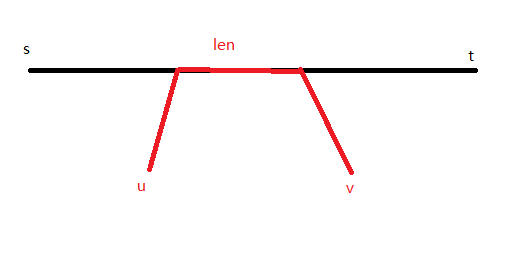
Snipaste_2021-03-03_09-44-08.png

\[ \ \]

求解

显然我们需要先知道 \(dis(u,v)\) ，可以 \(O(n)\) 预处理，我们选择的非树边一定满足 \(dis(u,v)>w\)

考虑抽直径构成序列 \(L_i\) ，然后考虑每一条非树边 \((u,v,w)\) 的贡献，设 \(u,v\) 在直径上对应根的编号为 \(x,y\)

确定非树边之后，我们需要选择一个最优的 \((s,t)\) ，答案计算上面已经提及

如果 \(x=y\) ，显然可以选择直径，下面讨论 \(x<y\) 的情况

  1. \((s,t)\) 与 \((u,v)\) 无交

1-1.对于 \((u,v)\) 之间的部分可以区间查询子树最值

1-2.两边预处理前缀/后缀最值

1-3.直径连接到 \(u\) ， \(v\) 子树的部分的答案

就是一棵树剔除根到一个点路径之后的直径长度，可以换根 \(dp\) 预处理

  1. \((s,t)\) 与 \((u,v)\) 有交，设交部分在直径上的区间为 \([l,r]\)

容易参分转化为求解： \(dis(s,t)+dis(u,v)-w-2(r-l)+2\) 最大值

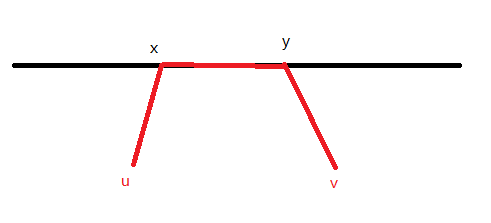
Snipaste_2021-03-03_09-58-39.png

2-1. 相交跨过直径上多个点

2-1-1.若 \(x<l<r<y\) ，此时容易用线段树维护答案

合并时减去跨过长度的贡献即可

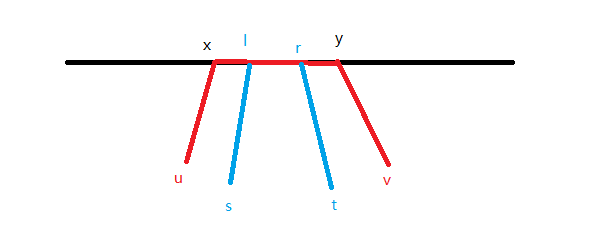
Snipaste_2021-03-03_10-00-38.png

2-1-2. 若 \(x<y , \text{and } (l=x \text{ or } r=y)\) ，此时显然两边部分最优一定是选择在直径上的部分

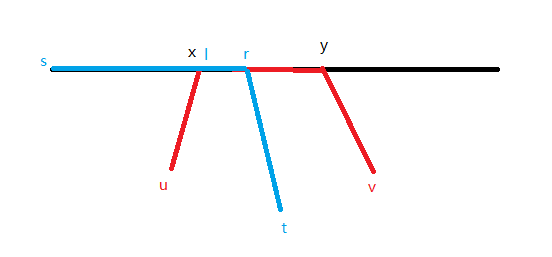
Snipaste_2021-03-03_10-01-17.png

以下情况一定不优

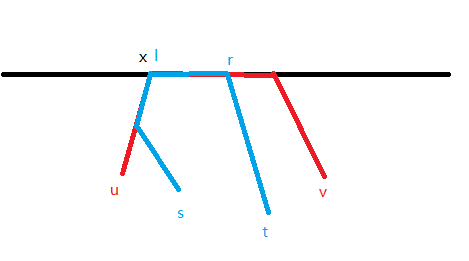
Snipaste_2021-03-03_10-03-49.png

另一边的答案可以在线段树上查询出来，是一个区间的前缀/后缀

2-2.若 \(l=r\) ，此时 \(l=x\) 或 \(l=y\) ，且在 \([u,x],[v,y]\) 部分有交

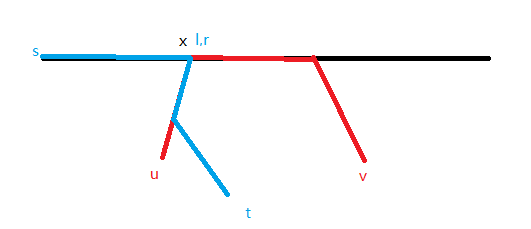
Snipaste_2021-03-03_10-05-43.png

容易发现，此时确定 \((s,t)\) 一边一定在直径的一端，另一端 \(x,y\) 对应的子树中

同样可以通过换根 \(dp\) 解决

区间查询，如果使用线段树解决，复杂度为 \(O(n+m\log n)\)

如果用奇怪数据结构（猫树），复杂度为 \(O(n\log n+m)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef pair <int,int> Pii;
#define reg register
#define mp make_pair
#define pb push_back
#define Mod1(x) ((x>=P)&&(x-=P))
#define Mod2(x) ((x<0)&&(x+=P))
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)
template <class T> inline void cmin(T &a,T b){ ((a>b)&&(a=b)); }
template <class T> inline void cmax(T &a,T b){ ((a<b)&&(a=b)); }

char IO;
template <class T=int> T rd(){
	T s=0; int f=0;
	while(!isdigit(IO=getchar())) f|=IO=='-';
	do s=(s<<1)+(s<<3)+(IO^'0');
	while(isdigit(IO=getchar()));
	return f?-s:s;
}

const int N=5e5+10,M=2e6+10,INF=1e9+10;


int n,m;
int U[M],V[M],W[M],D[M],vis[N];

struct Edge{
	int to,nxt;
} e[N<<1];
int head[N],ecnt;
void AddEdge(int u,int v){
	e[++ecnt]=(Edge){v,head[u]};
	head[u]=ecnt;
}

int ma,num,fa[N],dep[N];
vector <Pii> G[N];
int Find(int x){ return fa[x]==x?x:fa[x]=Find(fa[x]); }
void dfs1(int u,int f){
	if(dep[u]>ma) ma=dep[u],num=u;
	vis[fa[u]=u]=1;
	for(Pii v:G[u]) if(vis[v.first]) D[v.second]=dep[u]+dep[v.first]-2*dep[Find(v.first)];
	for(int i=head[u];i;i=e[i].nxt) {
		int v=e[i].to;
		if(v==f) continue;
		dep[v]=dep[u]+1,dfs1(v,u);
	}
	fa[u]=f;
}
void dfs2(int u,int f){
	if(dep[u]>ma) ma=dep[u],num=u;
	fa[u]=f;
	for(int i=head[u];i;i=e[i].nxt) {
		int v=e[i].to;
		if(v==f) continue;
		dep[v]=dep[u]+1,dfs2(v,u);
	}
}

int id[N],L[N],C,dp[N][2],dp2[N],g[N],h[N];
int subid[N];

void dfs3(int u,int f){
	fa[u]=f;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(id[v]||v==f) continue;
		dfs3(v,u);
		cmax(dp2[u],dp2[v]);
		int t=dp[v][0]+1;
		if(t>dp[u][0]) dp[u][1]=dp[u][0],dp[u][0]=t;
		else cmax(dp[u][1],t);
	}
	cmax(dp2[u],dp[u][0]+dp[u][1]);
}
void dfs4(int u,int f,int d=0){
	dep[u]=d,subid[u]=d<=1?u:subid[f];
	int tg[2]={-INF,-INF},th[2]={0,0};
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(id[v]||v==f) continue;
		int x=dp[v][0]+1-(d?d:1e9);
		if(x>tg[0]) tg[1]=tg[0],tg[0]=x;
		else cmax(tg[1],x);

		x=max(dp2[v],dp[v][0]+1);
		if(x>th[0]) th[1]=th[0],th[0]=x;
		else cmax(th[1],x);
	}
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(id[v]||v==f) continue;
		h[v]=max(h[u],th[0]==max(dp2[v],dp[v][0]+1)?th[1]:th[0]);
		g[v]=max(g[u],tg[0]==dp[v][0]+1-(d?d:1e9)?tg[1]:tg[0]);
		id[v]=id[u],dfs4(v,u,d+1);
	}
	if(f) cmax(g[u],dp[u][0]-d);
	cmax(h[u],dp2[u]);
}

struct Node{
	int len,ans,l,r;
	Node operator + (const Node __) const {
		Node res; res.len=len+__.len;
		res.ans=max(ans,__.ans);
		res.l=max(l,__.l-len),res.r=max(r-__.len,__.r);
		cmax(res.ans,r+__.l+1);
		return res;
	}
} s[N<<2];
void Build(int p,int l,int r) {
	if(l==r) {
		s[p]=(Node){1,max(dp2[L[l]],dp[L[l]][0]),dp[L[l]][0],dp[L[l]][0]};
		return;
	}
	int mid=(l+r)>>1;
	Build(p<<1,l,mid),Build(p<<1|1,mid+1,r);
	s[p]=s[p<<1]+s[p<<1|1];
}
Node Que(int p,int l,int r,int ql,int qr){
	if(ql<=l && r<=qr) return s[p];
	int mid=(l+r)>>1;
	if(qr<=mid) return Que(p<<1,l,mid,ql,qr);
	if(ql>mid) return Que(p<<1|1,mid+1,r,ql,qr);
	return Que(p<<1,l,mid,ql,qr)+Que(p<<1|1,mid+1,r,ql,qr);
}
int ls[N],rs[N];

int main(){
	n=rd();
	rep(t,1,rd()){
		int u=rd()+1,v=rd()+1,w=rd();
		if(w==1) AddEdge(u,v),AddEdge(v,u);
		else U[++m]=u,V[m]=v,W[m]=w,G[u].pb(mp(v,m)),G[v].pb(mp(u,m));
	}
	ma=-1,dfs1(1,0);
	ma=-1,dep[num]=0,dfs2(num,0);
	for(int u=num;u;u=fa[u]) L[id[u]=++C]=u;
	rep(i,1,C) dfs3(L[i],0),g[L[i]]=-INF,dfs4(L[i],0);
	rep(i,1,C) ls[i]=max(ls[i-1],i-1+dp[L[i]][0]);
	drep(i,C,1) rs[i]=max(rs[i+1],C-i+dp[L[i]][0]);
	Build(1,1,C);

	int ans=C-1;
	rep(i,1,m) if(D[i]>W[i]) {
		int u=U[i],v=V[i],d=0;
		if(id[u]>id[v]) swap(u,v);
		if(id[u]==id[v]) d=C-1;
		else {
			if(fa[u]) {
				cmax(d,h[u]);
				int f=subid[u],t=fa[f];
				cmax(d,id[u]-1+(dp[f][0]+1==dp[t][0]?dp[t][1]:dp[t][0]));
				cmax(d,id[u]-1+g[u]+2);
			} else cmax(d,dp[u][0]+id[u]-1);
			if(fa[v]) {
				cmax(d,h[v]);
				int f=subid[v],t=fa[f];
				cmax(d,C-id[v]+(dp[f][0]+1==dp[t][0]?dp[t][1]:dp[t][0]));
				cmax(d,C-id[v]+g[v]+2);
			} else cmax(d,dp[v][0]+C-id[v]);
			cmax(d,ls[id[u]-1]),cmax(d,rs[id[v]+1]);

			int g1=id[u]-1,g2=C-id[v];
			cmax(d,g1+g2-(id[v]-id[u])+2);
			if(id[u]+1<id[v]) {
				Node t=Que(1,1,C,id[u]+1,id[v]-1);
				cmax(d,t.ans);
				cmax(d,t.l+g1+1);
				cmax(d,t.r+g2+1);
			}
		}
		cmax(ans,D[i]-W[i]+d);
	}
	printf("%d\n",2*(n-1)-ans);
}