Equilateral Triangles

Posted on Edited on In

Equilateral Triangles

题意: 求所有三个点哈密顿距离相等的无序三元点对个数

推论1: 到平面中一点 \((x,y)\) 哈密顿距离为 \(d\) 的点，构成一个以 \((x,y)\) 为中心， \(d\) 为半对角线长的菱形

菱形不好搞，转一下，令旋转后的点 \(x'=x+y,y'=x-y\) ，(也就是曼哈顿距离转切比雪夫距离)

这样得到的就是一个正方形了

推论2: 选出的三点中，一定存在两个点 \(x\) 或者 \(y\) 坐标相同

如果选出点 \(A,B\) 不满足，由下图可以看到，可行的部分(就是相交部分 \(C1,C2\) )也必然满足

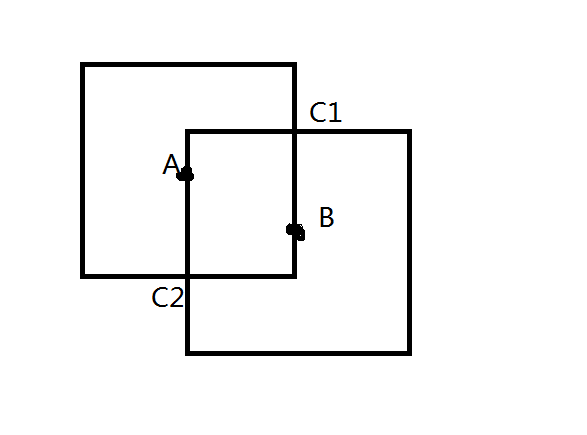
te1.png

接下来以 \(x\) 相同为例，枚举点 \(A,B\) ，设其距离为 \(d\)

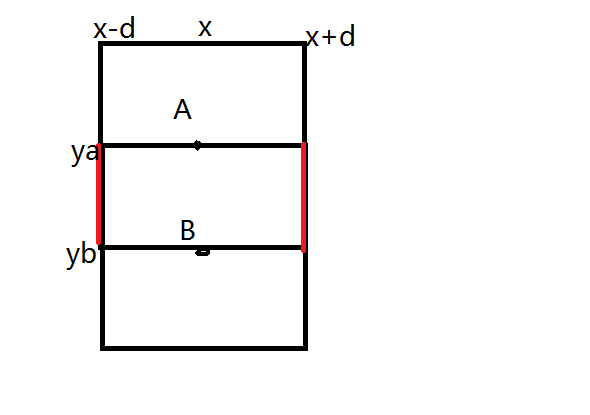
te2.png

可以看到比较显然就是两条红色的相交线段， \(O(n^3)\) 枚举 \(A,B\) 两点后，直接用前缀和维护即可

对于 \(x\) 相同，对于 \(y\) 相同分别做一次即可，注意考虑的时候不要把 \(x,y\) 都有相同的算两次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize(2)
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)

const int N=610;

int n;
char A[N][N],B[N][N];
int S[N][N];
int D[N],C;

int main() {
	scanf("%d",&n);
	rep(i,1,n) {
		scanf("%s",A[i]+1);
		rep(j,1,n) if(A[i][j]=='*') B[i+j][i-j+n]=1;
	}
	int ans=0;
	rep(i,1,n*2) rep(j,1,n*2) S[i][j]=S[i][j-1]+B[i][j];
	rep(i,1,n*2) {
		C=0;
		rep(x,1,n*2) if(B[i][x]) D[++C]=x;
		rep(a,1,C) rep(b,a+1,C) {
			int d=D[b]-D[a];
			i-d>=1 && (ans+=S[i-d][D[b]]-S[i-d][D[a]-1]);
			i+d<=n*2 && (ans+=S[i+d][D[b]]-S[i+d][D[a]-1]);
		}
	}
	rep(i,1,n*2) rep(j,1,n*2) S[i][j]=S[i][j-1]+B[j][i];
	rep(i,1,n*2) {
		C=0;
		rep(x,1,n*2) if(B[x][i]) D[++C]=x;
		rep(a,1,C) rep(b,a+1,C) {
			int d=D[b]-D[a];
			i-d>=1 && (ans+=S[i-d][D[b]-1]-S[i-d][D[a]]);
			i+d<=n*2 && (ans+=S[i+d][D[b]-1]-S[i+d][D[a]]);
		}
	}
	printf("%d\n",ans);
}