「2020NOIP模拟题-广大附中」C
「2020NOIP模拟题-广大附中」C
首先分析单对于LIS,LDS简单分析一下性质
不妨把选出的每个数 \(i,a_i\) 视为一个二维坐标系上的点,则显然在最优方案中
对于任意相邻的数,以 \((i,a_i),(i+1,a_{i+1})\) 为顶点的矩形中不存在在任何一个未被选择的点
接下来分析选出的两个序列:
推论1:两个方案的位置关系
这两个序列不论是在 \(x\) 还是在 \(y\) 上都不能被剖成两个分离的段
实际上作出两条描述方案的折线,它们必然有交点
推论2:交点的性质
只有两种情况,其中一种为

相交的两个相邻折线,构成的矩形一定是这样的
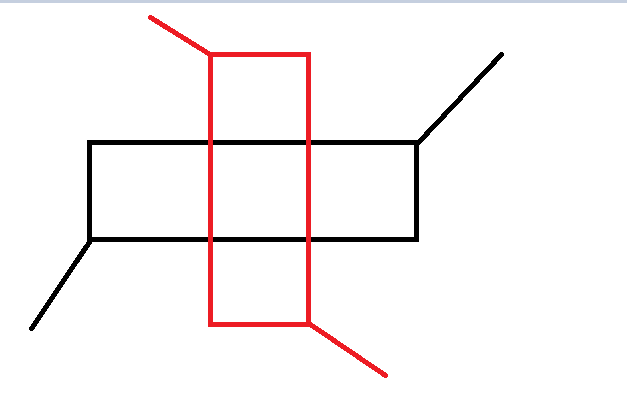
即分别在 \(x,y\) 上的范围有一个包含另一个
以这个交点为界,两个取出的序列值域独立,只需要找到这样的交叉处即可得到答案
接下来的问题分两步
Part1 找到候选折线
对于LIS来说一个点的转移前驱构成一个递减的子序列,显然我们需要找到这个序列中下标最小的
LDS相反
用树状数组即可
Part2 判断是否合法
满足两个维度上分别包含看起来像是一个奇怪的二维问题
但是实际上可以现,不管是LIS还是LDS,在查询的矩形中间是不会出现点的
所以可以转化为二维区间前缀问题,用离线树状数组解决
具体的,不妨对于LIS来考虑,设选出的点为 \((x,a_x),(y,a_y)\)
设候选的LDS折线为 \((u,a_u),(v,a_v)\)
我们需要知道的就是在下标上满足 \(v<y,u>x\)
在值上满足 \(a_u>a_y,a_v<a_x\)
可以分成4次查询完成,但是实际操作时和这个式子略有不同,见代码
存在两种包含关系,还需要反过来再做一次