给定 \(n\) 个点无向带权完全图，求将这些点分组，使得 组内的边边权 都小于 组内点连到组外点的边权
保证边权不同
考虑如何确定合法的分组
从小到大依次加入每一条边，则一个合法的分组一定在某一个时刻满足
1.这个分组是一个极大的连通块
2.这个分组是一个团
考虑类似 \(\text{Kruskal}\) 重构树的方法，对于合并的过程转化为树形结构
此时，分组决策只有两种
1.这个点儿子内部分别分组，背包合并
2.如果这个点恰好是合法的分组，那么选择这个点建立新的分组，并且此时儿子必须都是散点
借用树形背包的复杂度分析， \(dp\) 部分复杂度为 \(O(n^2)\)
排序可以桶排
1 |
|
有一个网格图 \(A\) ，每个点有一个方向 \(D_{i,j}\) 和一个权值 \(A_{i,j}>0\) ，其中方向指向四联通的某一个点
定义其生成网格图为 \(B\) ，每个点的权值为这个点能够到达的点权值之和
现在给定 \(B\) ，构造一个 \(A\)
每个点一条出边的图是基环内向树，环上的点 \(B_{i,j}\) 相同，树上点权值 \(B_{i,j}>B_{fa_{i,j}}\)
那么对于 \(B\) 中的点，如果能够找到周围一个 \(B_{i',j'}<B_{i,j}\) ，则可以认为 \((i,j)\) 已经确定了方向
否则，周围必须存在点 \(B'_{i,j}\) 与 \(B_{i,j}\) 相同构成环
考虑网格图上不存在奇环，那么可以把环分解为若干极小的二元环，这样的构造是最优的
于是问题降低为二元，变成一个二分图匹配问题，具体的
给定 \(n\) 个点 \(P_i\) ，在每个点对之间连一条线 \(P_iP_j\)
求所有线到原点距离的第 \(k\) 小
这个 \(k\) 大问题的 \(k\) 是 \(O(n^2)\) 级的，因此不是调整，可以考虑二分答案 \(L\)
考虑如何确定 \(d(O,P_iP_j)>L\) ，容易发现这等价于
\(P_iP_j\) 与圆 \(C:x^2+y^2=L^2\) 无交
假设当前确定了 \(P_i\) ，考虑什么时候 \(P_j\) 是合法的
灰色线是切线，用蓝色区域标出了 \(d(O,P_iP_j)>L\) 的范围
直接统计蓝色区域的点并不容易，考虑对于这些点也作切线
容易发现这些点的两个切点恰好被 \(P_i\) 的两个切点分隔开
通过求切点角度，转化为二维区间问题，用树状数组解决
复杂度为 \(O(n\log n\log x)\) ，其中 \(x\) 为精度范围
1 | const int N=2e5+10,INF=1e9+10; |
给定一个 \(2n\times 2m\) 的交错棋盘，一个位置 \((i,j)\) 可以放当且仅当 \(2|i+j\)
给定 \(q\) 次操作，每次操作在一个位置加入或删除一个障碍
求是否存在一种方案能在棋盘上放入 \(nm\) 个互不攻击的国王（国王走九宫格）
棋盘是交错的减少了很多无法处理的情况
容易发现，任何一个King都只能在它自己 \(2\times 2\) 的小方格内选择两种位置
如果一个 \(2\times 2\) 的单元左上角被填了，那么它就只能选择右下角
而根据这个King的互斥位置，在其右下方的所有King都只能选择右下角
如果右下角被占了同理，左上方的King只能选择左上角
实际上判定是否有解就是判定这些关系是否互斥，将每个点按照其所属 \(2\times 2\) 单元编号
则问题转化为一个检查二维偏序的问题
删点容易通过线段树分治转化，偏序可以用树状数组处理
1 | const int N=2e5+10,P=998244353; |
给定一个均分成 \(n\) 份( \(n\) 为偶数)的圆，每份上有一个元素为0/1，其中一些元素的值未知，且随机
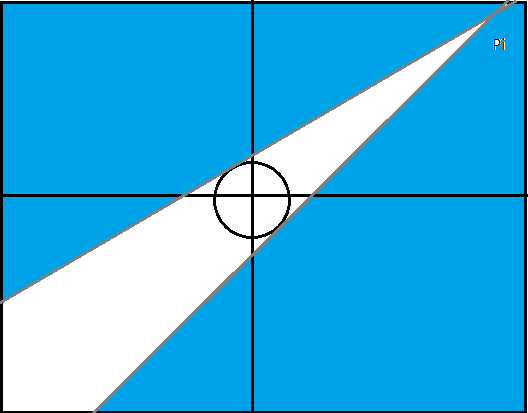
当存在一个方案，0和0连线，1和1连线，使得每个元素都被恰好连一条线时，称环 \(c\) 合法
定义 \(f(c)\) 为上述连线方案中 不同色连线交叉的最小次数
同时需要支持修改元素，求 \(f(c)\) 的期望
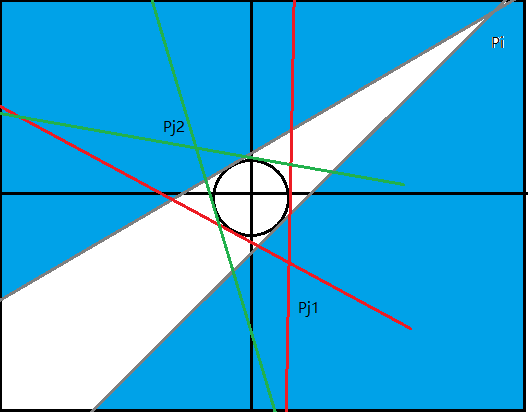
首先考虑一个Naive的贪心，在环上一旦出现相邻两点同色，就将他们连线然后删除
直到最后，就将变成01交替，设此时环长 \(n'\) ，考虑再让相邻的00,11连线
则得到交叉个数为 \(\frac{n'}{4}\)
这个贪心甚至连不带修的情况都做不了
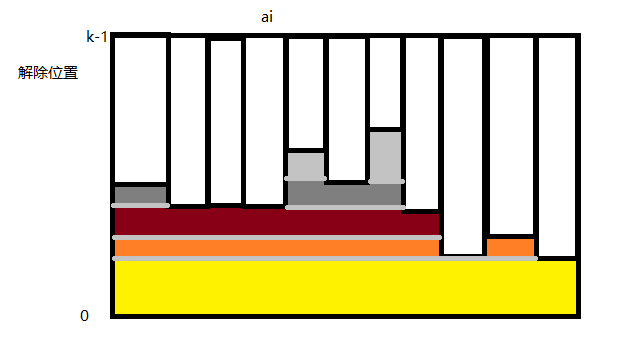
考虑上面贪心过程中被抵消的点
容易发现一定是一个奇数位置的点去抵消一个偶数位置的点
并且抵消之后其他位置的奇偶性保持不变
因此猜想最终剩下的黑点数量就是 \(|cnt_{odd}-cnt_{even}|\)
其中 \(cnt_{odd},cnt_{even}\) 表示已经确定的1元素在奇数/偶数位上的个数
也容易证明
根据贪心，显然同奇偶的点无法抵消，因此 \(ans\ge |cnt_{odd}-cnt_{even}|\)
而一旦存在两个不同奇偶的黑点，若他们不相邻
则他们之间一定存在一对相邻白点（否则奇偶性不对），进而不断合并白点使得它们相邻
白点可以对称得到相同值的式子，最终得到答案就是
\(\displaystyle \frac{|cnt_{odd}-cnt_{even}|}{2}\)
设已经确定的部分 \(\delta=cnt_{odd}-cnt_{even}\) ，未确定的部分包含 \(x\) 个奇数位置， \(y\) 个偶数位置
则Naive的计算答案式子为
\(\displaystyle Sum=\sum_{i=0}^x \sum_{j=0}^y \frac{1}{2}\cdot [2|i-j+\delta] \cdot |\delta+i-j|\binom{x}{i}\binom{y}{j}\)
NTT
补上方案数 \(2^{x+y-1}\) （因为只有一半的方案奇偶性相同），用 \(y-j\) 代换 \(j\)
\(\displaystyle E=\frac{1}{2^{x+y}}\sum_{i=0}^x \sum_{j=0}^y \cdot [2|i-y+j+\delta] \cdot |\delta+i-y+j|\binom{x}{i}\binom{y}{j}\)
转换为 \(\displaystyle i+j\leftarrow \binom{x}{i}\binom{y}{j}\) 的形式后，带入组合意义合并 \(i,j\)
\(\displaystyle E=\frac{1}{2^{x+y}}\sum_{i=0}^{x+y} \cdot [2|\delta-y+i] \cdot |\delta-y+i|\binom{x+y}{i}\)
不妨设 \(\delta'=\delta-y\)
\(\displaystyle E=\frac{1}{2^{x+y}}\sum_{i=0}^{x+y} \cdot [\delta'\equiv i\pmod 2] \cdot |\delta'+i|\binom{x+y}{i}\)
根据 \(\delta'+i\) 的正负性容易确定一个范围，范围两边都是计算都转化为
\(\displaystyle S(n,m)=\sum _{i=0}^m [2\not |i]\cdot i\cdot \binom{n}{i}\)
\(\displaystyle S(n,m)=\sum _{i=0}^m [2\not |i]\cdot n\cdot \frac{(n-1)!}{(n-i)!(i-1)!}\)
\(\displaystyle S(n,m)=n\sum _{i=0}^{m-1} [2 |i]\cdot \binom{n-1}{i}\)
形如 \(\displaystyle m|2, S'(n,m)=\sum _{i=0}^m [2|i]\cdot \binom{n}{i}\) ，可以转化为
\(\displaystyle S'(n,m)=\sum _{i=0}^m [2|i](\binom{n-1}{i}+\binom{n-1}{i-1})\)
\(\displaystyle S'(n,m)=\sum _{i=0}^m \binom{n-1}{i}\)
组合数关于 \(m\) 一维的前缀和是一个经典的步移问题
\(S(n,m-1)=S(n,m)-C(n,m)\)
\(S(n,m+1)=S(n,m)+C(n,m+1)\)
\(S(n+1,m)=\displaystyle \sum_{i=0}^m C(n+1,m)=\sum_{i=0}^mC(n,i)+\sum_{i=0}^{m-1}C(n,i-1)=2S(n,m)-C(n,m)\)
\(\displaystyle S(n-1,m)=\frac{S(n,m)+C(n-1,m)}{2}\)
封装一下计算即可，复杂度为 \(O(n)\)
真的只是一点点麻烦
1 |
|
给定一个置换 \(p_i\) ，求通过最少次交换 \(p_i,p_j\) ，使得最终的置换中所有置换环 \(size\) 乘积最大
一个常规结论：
对于 \(n(n\ge 3)\) 的拆分 \(n=\sum_{i=1}^m a_i\) ，最大化 \(\prod a_i\) ，最优情况下
\(n\mod 3=0\) ， \(a_i=3\)
\(n\mod 3=2\) ， \(i<m,a_i=3 ; a_m=2\)
\(n\mod 3=1\) ， \(i<m,a_i=3 ; a_m=4\) 或 \(i<m-1,a_i=3 ;a_{m-1}=a_m=2\)
容易发现对于任意 \(n\) ，最终 \(a_i\) 的方案是 \(O(1)\) 的，设当前置换环为 \(b_i\) ，我们需要操作 \(b_i\) 变成 \(a_i\)
1.一次在同环交换可以分裂一个环
2.一次异环交换合并两个环
所以原问题实际上就是最少次数分裂合并 \(b_i\)
对于 \(n\mod 3=0\) 或 \(n\mod 3=2\) 的情况，如果当前 \(b_i\ge 3\) ，可以一直不停分裂
最终剩下的就是 \(b'_i=1\) 或者 \(b'_i=2\)
对于 \(n\mod 3=2\) 的情况，优先从中取出一个2<或者由两个1合并得到一个2
剩下的优先合并1和2，然后剩下的自己合并
\(n\mod 3=1\) 同理，但是 \(a_i=4\) 的情况也不能分裂，需要拿出来特殊处理
1 | const int N=1e6+10,P=1e9+7; |
A和B在树上Van游戏，每个人操作一些点
A操作一个点 \(i\) ，B操作一个点集 \(a_j\)
每轮A,B分别进行操作，可以对于自己的所有点任意移动1步或0步
在某一轮，当A的点碰到B的点时游戏结束
A希望尽量迟结束，B希望尽量早结束
给定B的初始点集 \(a_j\) ，对于A的每个初始点 \(i\) 判断多少轮结束
由于B的操作显然是不停向A收缩直到碰到
那么可以广搜求出每个点原地不动时被B干掉的时间 \(F_i\)
那么考虑A的移动过程，每一步可以到达一个点 \(u\)
必须满足在第 \(i\) 步所在的点 \(u\) ， \(F_u>i\) ，否则结束游戏
对于初始节点 \(u\) ，不妨设最终结束的节点为 \(t\) ，我们希望一路跑到 \(t\) 然后站住不动，此时答案就是 \(F_t\)
而实际上，任何一个点 \(u\) 能够跑到 \(t\) ，等价于 \(dis(u,t)<F_t\)
Proof:
由最短路三角不等式可知
\(\forall (u,v)\in Tree, dis_{v}-1\leq dis_u\leq dis_{v}+1\)
即 \(dis_e\) 在树的路径上连续变化，不妨设移动路径为 \(p_i,i\in[1,k],p_k=t,k\leq F_t\)
若能在 \(F_t-1\) 的时间内到达 \(p_k\) ，那么必然能在 \(F_t-2\) 的时间内到达 \(p_{k-1}\)
进而归纳得到
那么问题变成了，对于每个点 \(u\) ，向周围 \(F_u-1\) 范围内的点对于 \(F_u\) 取 \(\max\)
容易点分治处理，复杂度为 \(O(n\log n)\)
1 | const int N=2e5+10,INF=1e9+10; |
对于一个序列 \(A\) ，一个合法的质因子序列 \(P\) 满足 \(\forall P_i|A_i,P_i\ is\ a\ prime\)
给定一个序列 \(a_i,i\in[1,n]\) ，求选出 \(k\) 个数，使得对于选出的序列 \(A\)
不存在一个 \(P\) 使得 \(P\) 中某个元素恰好出现一次
\(n\leq 1000,a_i\leq 10^{18}\)
由题目的意思我们知道肯定要分解质因数
Pollard's_Rho!!!
\(10^{18}\) 分解质因数可不是开玩笑的。。。
所以先考虑合法 \(A\) 的判定
假设可以存在一个元素恰好出现一次 \(x\) ，那么在 \(A\) 所有元素质因子中至少要包含一个 \(x\)
并且，不存在两个元素只包含 \(x\)
也就是说，对于合法的 \(A\) 中出现的所有质因子 \(x\) ，都必须存在两个元素只包含 \(x\)
我们称只包含 \(x\) 作为质因子的元素为 \(x\) -元素，为了构造合法的 \(A\) ，我们必须对于一些 \(x\) 选出若干对 \(x\) -元素
对于每个 \(x\) ，我们只把前两个 \(x-\) 元素视为有效，假设有 \(c\) 对这样的元素
那么情况分几种
\(2|k,2c\ge k\) ，那么直接随意选完即合法
\(2c\ge k,2\not |k\) ，此时我们需要选出部分对，使得剩下的元素中存在一个数它的因子集已经被选
枚举剩下一个元素，判定合法即可
亲身试验，我的Pollards_Rho它T飞了
容易发现，对于 \(x-\) 元素我们只需要找到它的 \(a_i=x^k\)
对于其他元素我们只需要找到 \(a_i\) 对应的 \(x\) 的集合，或者判断无法被 \(x-\) 元素集合包含
由于 \(n\leq 1000\) ，我们可以先得到 \(x-\) 元素集合，其他元素我们最后一个个判定
找到 \(a_i=x^k\) 问题简化了很多
如果你相信std::pow，可以直接来
只需要找到一个最小的 \(k'\) ，使得 \(a_i=x'^{k'}\) ，判定 \(x'\) 是否为质数，如果是则停止，否则继续分解 \(x'\)
对于 \(k'\leq 3\) ，甚至更大一些的情况，std::pow比较可信
而 \(k'>3\) 的情况（实际上 \(k'=4\) 被 \(k'=2\) 包含，所以是 \(k'\ge 5\) ）
实际上 \(x'\) 已经很小了，直接枚举质数即可
素数判定依然需要 \(\text{Miller_Rabin}\)
，但是至少不用Pollards_Rho了
1 | const int N=1e5+10; |
有 \(n\) 个二进制数 \(a_i\in[L_i,R_i]\) ，给定每个二进制位的权值
序列 \(a_i\) 的权值就是 \(a_i\oplus a_{i+1}\) 二进制为权值之和
求所有满足 \(a_i\in[L_i,R_i]\) 的最小权值
显然需要我们考虑对于一个数进行 数位 \(dp\) 的过程
从高位到低位，一个数要么最终都一直被限制着，要么在两个不同的位置分别解除了 \(L_i,R_i\) 的限制
容易发现， \(L_i,R_i\) 中某一个先被解除的限制一定是在第一个 \(\text{bit}(L_{i},p)\ne \text{bit}(R_i,p)\) 的位置 （实际上是小于号）
此后，选择的数一直跟着剩下的限制直到下一个位置解除
不妨考虑 \(L_i,R_i\) 中限制时间较长的一个限制，设在 \(p\) 这一位解除，那么
2.如果是 \(R_i\) ，那么 \(\text{bit}(R_i,p)=1,\text{bit}(a_i,p)=0\)
如果是 \(L_i\) ，那么 \(\text{bit}(R_i,p)=0,\text{bit}(a_i,p)=1\)
如果最终每个数解除限制的位置如下
考虑他们如何对于答案贡献
对于每个二进制位，如果存在空白段，空白段的二进制可以跟随左边的段或者右边的段改变
当左边和右边最邻近的两个数这一位不同，则产生贡献
因此考虑依次扫描每一个二进制位，找到相邻可能产生贡献的 \((a_l,a_r)\)
从低位到高位，这就是一个不断将 \((a_l,a_r)\) 分裂为 \((a_l,a_k),(a_k,a_r)\) 的过程
也就是一个 笛卡尔树上的区间dp
对于当前二进制位 \(p\) 和数对 \(a_l,a_r\) ，我们需要知道的是
\(a_l\) 是受到 \(L_l\) 还是 \(R_l\) 的限制，且是否 \(p\) 这一位它解除了限制 （因为解除贡献的这一位与 \(L_l / R_l\) 相反）
\(a_r\) 是同理
转移可以直接进入下一个二进制位，计算 \(a_l,a_r\) 的贡献
或者分裂区间枚举中点 \(k\) ， \(a_k\) 恰好在这一位解除限制（或者 \(a_k\) 一直都没有解除限制，此时 \(p=0\) ）
此时 \(L_k,R_k\) 必然满足前面提到的限制，并且根据 \(\text{bit}(L_k,p)\) 和 \(\text{bit}(R_k,p)\) 枚举 \(k\) 受到 \(L_k\) 或者 \(R_k\) 的限制
1 | const int N=55; |
有两队人 \(a_i,i\in[1,n],b_j,j\in[1,m]\) ，现在把他们放在一起排成一行 \(c_i\)
顺次给每个人计分，初始 \(s_0=k\)
\(s_i=\max\{0,s_{i-1}+c_i-c_{\max\{i-1,1\}}\}\)
现在要最大化每个 \(a_i\) 所在位置的 \(s_i\) 之和 与 \(b_i\) 所在 \(s_i\) 之和 的差
支持修改和对于不同 \(k\) 查询
考虑 \(k=0\) 简单情况
1.若 \(s_i\) 不清零，则 \(s_i=c_i-lst\) ，其中 \(lst\) 表示上一个被清零位置的 \(c_j\)
容易发现， \(\displaystyle s_i=c_i-\min_{j\leq i}\{ c_j\}\)
那么对于含 \(k\) 的情况，类似可以得到
\(\displaystyle s_i=k-c_1+c_i+\max\{0,c_1-k-\min_{j\leq i}\{c_j\}\}\)
假设我们固定了一个 \(c_1\) ，现在考虑对于剩下的 \(a_i,b_j\) 排出一个最优的排列
容易发现， \(k-c_1+c_i\) 的贡献时固定的，只有前缀最小值会影响答案
我们希望对于 \(b_i\) ，前缀最小值较大， \(a_i\) 反之
那么容易发现可以先降序排列 \(b_j\) ，再正序排列 \(a_i\)
此时 \(b_{\min}\) 可以贡献给 \(a_i\) 的前缀最小值，同时 \(b_j\) 的前缀最小值能够取到最大
此时，不妨设 \(c_1=t\) ， \(\min\{a_i,b_i\}=Min\)
在 \(\min\{c_j\}=c_1\) 时， \(\max\) 里的东西没有贡献，故可以得到
1.对于每个 \(a_i\) ，若它没有被放在 \(c_1\) ，则贡献 \(k-t+a_i+\max\{0,t-k-Min\}\)
2.对于每个 \(b_i\) （不特殊考虑第一个），则贡献 \(-(k-t+b_i+\max\{0,t-k-b_i\})\) （忽略最小值为 \(t\) 的情况）
则最终式子为
\(\displaystyle f(t)=(n-[t\in a_i])\cdot \max\{0,t-k-Min\}-\sum \max\{0,t-k-b_i\}+(m-n)t+C\)
其中 \(C=(n-m)k+\sum a_i-\sum b_i\)
容易发现 \(f(t)\) 是关于 \(t\) 的分段一次函数，根据斜率变化情况分析，极值位置仅 \(O(1)\) 个
那么对于 \(a_i\) 作为 \(t\) 和 \(b_j\) 作为 \(t\) 的情况，分别计算 \(f(t)\) 的极值位置
极值位置需要一个 \(k\) 大查询和 \(\text{lower_bound}\)
计算 \(f(t)\) 需要一个前缀查询
我用 \(\text{BIT}\) 充当平衡树来维护，复杂度为 \(O((n+m+q)\log 10^6)\)
1 | const int N=1e6+10,INF=1e9+10; |